「判断推理」はできるけど、「数的推理」は苦手だし嫌い。
図形の計量なんて、補助線をどこに引けばいいのかわからない。
でも、「数的推理」を捨てるのはヤバイ気がするし……。

こんな悩みをお持ちではないでしょうか。

本稿では、どうすれば数的処理における「数的推理」を得点源にできるか、基本から徹底解説いたします。
ぜひ参考にして、「数的推理」の苦手意識から開放されてください！

数的推理とは？

数的推理とは、「数的処理」の中にある1つの分野を指し、公務員として必要な事務処理能力を問う問題になります。

数的処理には、判断推理・数的推理・資料解釈の3分野があります。
ただし、判断推理に含まれる図形問題を別途「空間把握」として、4分野と説明する場合もあります。

「数的推理」は、問題文を読み込み、論理的に思考・計算して、そこから短時間で答えにたどり着くことが求められます。

数の性質、約数・倍数、場合の数、確率、比と割合、濃度、速さ、最大・最小、二次関数、図形の長さ・角度・面積・体積を求める問題などから出題されます。
確率と図形はどの職種でもほぼ確実に出題されます。

出題分野は以下のとおりです。（分類の仕方は諸説あります）

• 約数・倍数
• 整数
• 比と割合
• 利益
• 濃度
• 記数法
• 数列
• 最大・最小
• 速さ
• 覆面算・魔方陣
• その他の文章題（ニュートン算、仕事算、集合算、年令算、平均算）
• 場合の数
• 確率
• 図形の計量

中学3年までの数学の教科書にあるようなテーマばかりです。

ただ、いずれも、「判断推理」や「資料解釈」よりも、数学的知識がストレートに必要とされるのが、苦手とする受験性が多い理由のようです。

※関連記事：【公務員試験の科目一覧】教養科目と専門科目とは？

数的推理は苦手だったら捨てるべきか？

このように、数的推理を苦手とする受験生は多いですが、他方で筆記試験は満点を取る必要はありません。

では、苦手な方は、いっそ数的推理を捨て科目とすべきでしょうか。

数的推理の勉強は、受験する公務員の職種によって勉強時間を変えることを推奨します。

まず、出題数から見てみましょう。

「数的推理」の出題数は、「判断推理」と同程度で、どちらかに極端に偏ることはないのが、一般的な傾向ですが、職種による違いはあります。

主な職種の「数的推理」の出題数です。

• 国家一般職　8問（図形1〜2問）
• 国家専門職（国税・財務・労基）　5問（図形1問含む）
• 東京都　5問（図形1〜2問含む）
• 東京特別区 6問（図形1〜2問）
• 裁判所事務官⼀般職　 6問（図形2問）
• 地方上級　自治体によっても異なるが、概ね6問（図形1〜2問）
• 市役所　5問（図形1問）

東京都や東京特別区は、一般知能の配点が高いので、数的推理を捨て科目にするのは危険です。

国家公務員も一般知能の配点が高いので、同様のことが言えます。
ただ、国家一般職は専門科目の配点が教養科目の2倍、国家専門職は1.5倍と、専門科目の比重が高いです。

これらの職種は、教養科目で高得点を目指す必要がないので、数的推理に捨てる分野があっても大丈夫です。

地方上級は、教養科目内における一般知能と一般知識が半々なので、仮に数的推理を捨て科目にしても、一般知識で点を稼ぐという戦略もとれます。

このように、職種によって、数的推理の勉強に時間をかけるべきかどうか、異なってくる傾向はあります。

苦手な方にとっては、数的推理は捨てて、他の分野・科目に力を入れるのも考えたくなるところではあります。

ただ、どの職種であっても、数的処理自体を捨て科目にはできません。

重要なのは、数的処理のどの分野の勉強に時間をかけるかです。

一般的に、判断推理は解き方がわかっても、解答を出すまでの作業に時間がかかる問題が多い傾向にあります。
これに対して、数的推理は、解き方がわかれば、解答までの作業に時間がかからない問題がほとんどです。

時間との戦いがシビアな教養試験にあって、本試験での1問あたりの解答時間は重要ポイントです。

数的推理の中でも、出題頻度の高い分野は、捨てることなく勉強する価値は高いといえます。

数的推理の過去問題を使った解き方のコツ

ここでは、地方上級で出題された過去問を使って、数的推理の解き方のコツを説明してみましょう。

制限時間は1問あたり3分です。

4ケタの正の整数A＝1000a＋100b＋10c＋dは、A＝9(111a＋11b＋c)＋(a＋b＋c＋d)と書ける。

これを利用し、4ケタの数6□7□が9で割り切れるときに、2つの□に入る数字の和を求めよ。

1　4のみ
2　5のみ
3　8のみ
4　4または12
5　5または14

答えと過去問の解説はこちら

【答え：5　5または14】

本問で、問題文を構成しているのは、
①「4ケタの数6□7□が9で割り切れるときに、2つの□に入る数字の和を求めよ。」
この部分だけです。

　

実際、この部分だけでも問題文として成立します。
これ以前の文章は、いわば解答のヒントです（そういう意味で親切な問題です）。

ところが、「これを利用し」とあるので、
②「4ケタの正の整数A＝1000a＋100b＋10c＋dは、A＝9(111a＋11b＋c)＋(a＋b＋c＋d)と書ける。」
この部分を考え込んでしまうと、泥沼です。ま、それが出題者の企みでもあるのですけどね。

　

実は、③「9の倍数は、各位の数字の和が9の倍数」というルールがあります（他の数字の倍数の見つけ方もありますが、ここでは割愛します）。

例えば、2574の各位の数字の和は2＋5＋7＋4＝18です。
18は9の倍数なので、2574は9で割り切れます。

③「9の倍数は、各位の数字の和が9の倍数」は暗記しておくべきルールなのです。

　

で、これを使って本問を解くと
①「4ケタの数6X7Yが9で割り切れるときに、2つの□に入る数字の和を求めよ。」
6X7Ｙが9の倍数ということは、6＋X＋7＋Yが9の倍数にならなければなりません。
→13＋X＋Y＝9の倍数

　

本問では、X、Yそれぞれの値は聞かれていません。
聞かれているのは、X＋Yなのにも注意してください。

あとは、選択肢の数字を順に入れていって、13と足して9の倍数になるものを探せばいいわけです。

答えは、5の「5または14」になります。

本問では、

1. 倍数の見つけ方の暗記
2. 問題文が何を聞いているのかを見逃さない
3. 選択肢の有効活用

といった、基礎知識と解法テクニックが必要なことがわかります。

あとは、素早く計算できるように反復練習です。
そうすれば、数的推理のほとんどの問題は、短時間で解くことができるようになります。

【出典：国家一般職】判断推理（論理式）の過去問と解説

ある研究室の学生について、次のことがわかっているとき、論理的に確実にいえるのはどれか。
　〇パソコンを持っていない人は、スマートフォンを持っている。
　〇デジタルカメラを持っている人は、プリンターを持っている。
　〇プリンターを持っている人は、パソコンを持っており、かつ、腕時計を持っている。
　〇スマートフォンを持っている人は、腕時計を持っていない。

１　スマートフォンを持っている人は、デジタルカメラを持っていない。
２　デジタルカメラを持っていない人は、パソコンを持っている。
３　パソコンを持っている人は、腕時計を持っている。
４　腕時計を持っている人は、プリンターを持っている。
５　プリンターを持っている人は、スマートフォンを持っている。

答えと解説はこちら

【答え：１　スマートフォンを持っている人は、デジタルカメラを持っていない。】

与えられた4つの命題を論理式で表すと、それぞれ以下のようになる。便宜上、1番目から4番目までの各命題をそれぞれア～エとする。
　ア　パソコン→スマートフォン
　イ　デジタルカメラ→プリンター
　ウ　プリンター→パソコン∧腕時計
　エ　スマートフォン→腕時計
これらにしたがって、各選択肢を検討する。

　

１　〇
　ウの対偶を取ると、「パソコン∨腕時計→プリンター」が導かれるので、「腕時計→プリンター」が成り立つ。また、イの対偶を取ると、「プリンター→デジタルカメラ」が導かれる。したがって、エより、「スマートフォン→腕時計→デジタルカメラ」が導出される。よって、「スマートフォン→デジタルカメラ」といえる。

　

２　×
　ア～エからは、デジタルカメラ→□　となる命題を導出することができない。

　

３　×
　ア～エからは、パソコン→□　となる命題を導出することができない。

　

４　×
　エの対偶を取ると、「腕時計→スマートフォン」が導かれる。また、アの対偶を取ると、「スマートフォン→パソコン」が導かれるので「腕時計→スマートフォン→パソコン」が導出される。しかし、肢３でみたように、「パソコン→□」となる命題を導出することができないので、この先を推論することができない。

　

５　×
　ウより、「プリンター→腕時計」が成り立つ。もっとも、肢４で見たように、エの対偶から、「腕時計→スマートフォン」が導かれるので、「プリンター→スマートフォン」が導出される。

　

【出典：市役所】判断推理（ペン式）の過去問と解説

ある幼稚園の園児に、犬、猫、ペンギンのそれぞれについて、「好き」まあは「好きでない」のいずれであるかを尋ねた。次のことがわかっているとき、確実に言えるのはれか。
　〇犬が好きな園児は、猫が好きでない。
　〇象が好きな園児は、ペンギンも好きである。
　〇猫が好きな園児の中には、象も好きな園児がいる。
　〇象が好きな園児の中には、犬も好きな園児がいる。

１　ペンギンだけが好きな園児がいる。
２　ペンギンが好きな園児は、犬、猫、象のいずれも好きである。
３　犬が好きでない園児は、象も好きでない。
４　犬も猫もどちらも好きでない園児は、象とペンギンのどちらも好きである。
５　犬が好きな園児の中には、ペンギンも好きな園児がいる。

答えと解説はこちら

【答え：５　犬が好きな園児の中には、ペンギンも好きな園児がいる。】

「Aな人は、Bである」というのは「Aな人は必ずBである」→「AはBに含まれる」というふうに言い換えられる。
これを考えながら、与えられて津の条件を言い換えていくと、
　・「犬好き」は「猫嫌い」に含まれる（犬好きと猫スキは排反）
　・「象好き」は「ペンギン好き」に含まれる
　・「猫好き」と「象好き」には共通部分があるが、互いを完全には含まない。
　・「象好き」と「犬好き」には共通部分があるが、互いを完全に含まない。

ペン図に整理すると以下のようになる。

　

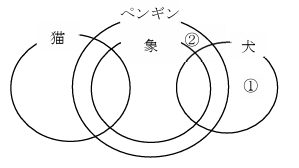
このとき、①（犬だけが好きな園児）及び②（ペンギンだけが好きな園児）の部分の要素は、0人である可能性がある。
①に関しては、「犬⊆ペンギン」となる可能性があり、②に関しては、「ペンギン∧象＝ペンギン∧犬∧象」となる場合や「ペンギン＝象」となる可能性があるからである。
　以上に基づいて、各選択肢を検討する。

　

１　×
　図の②部分に関しては、上述したように不確定であるので、ペンギンだけが好きな園児が必ずいるとまではいえない。

　

２　×
　図より、ペンギンが好きな園児であっても、犬、猫、象のいずれも好きであるとはいえない。

　

３　×
　図より、犬が好きでない園児であっても、象が好きである場合がある。

　

４　×　
　図の②部分に関しては、上述したように不確定であるので、ペン着だけが好きな園児がいる可能性がある。

　

５　〇
　図より、犬が好きな園児のなかには、ペンギンも好きな園児がいるといえる。

　

数的推理の勉強法～解放パターンの暗記～

本試験では1問あたりの平均時間は3〜4分です。

このような短時間で解答にたどり着くためには、

• 問題文を見て瞬時に解法が思いつく
• 作業（計算など）を素早く行う

ことが必須です。

そのため、「解法パターンの暗記」と「作業を素早く行うための練習」が必要です。
「数的推理」に限らず、数的処理の勉強に必要なのは知識と反復練習というのは、ここから来ているわけです。

数的推理に必要な数学の知識は、基本的には中学〜高校1年までで学ぶ基礎的なもので足ります。
具体的には、以下の項目が該当します。

• 約数・倍数
• 整数
• 比と割合
• 関数（一次関数・二次関数：最大値・最小値の求め方）
• 方程式（一次方程式・二次方程式・不等式）
• 記数法
• 数列
• 場合の数・確率
• 図形に関しては、比、三平方の定理、相似と合同、平行線の性質・面積・体積の公式

これらの知識を忘れた方は、中学3年間の数学を1冊にまとめたコンパクトな書籍などで復習するといいでしょう。

さらに、計算を早く行うための知識も重要ポイントです。
次の問題を考えてみましょう。

新幹線は1両の長さは25メートルです。
16両編成の新幹線の全長は何メートルか？

もちろん、こんな単純な計算問題は出題されません（残念？）。

大切なのは、この程度の計算なら暗算で即答できるかです。

これを解くのに、25×16と筆算していると答えはでますが、時間がかかります。

前提として、「25の４倍は100」と暗記しておきます。

すると、16両÷4両＝4
4両×100＝400
16両編成の新幹線の全長は400メートルと瞬時に答えが出ます。

他にも、

11²＝121、12²＝144、13²＝169……
Aの5倍は、Aの半分の10倍。例えば、12の5倍は、12の半分の6の10倍で、60。

といったように、掛け算の九九を暗記するのと同様に、よく出てくる計算を暗記したり、合理的な計算方法を知っておくと、楽に速く計算ができます。

このようにして、知識の引き出しを作った後は、問題文に応じてどの引き出しを使うかを瞬時に考えつくように、過去問で反復練習です。

過去問は、式を立てるだけでなく、最後まで計算するようにしてください。

よく、「式は立てられるけど計算ができない」という方がいます。
これは、反復練習が足りないだけです。

日頃からスマホの計算機に頼って暗算する機会が減っているのも弊害になります。
本試験までは、極力計算機を封印して暗算するようにするだけでもいい訓練になります。

※関連コラム：【公務員試験】数的処理の勉強法やコツとは？どんな問題が出る？

【最新】数的推理の過去問【国家・地方公務員】

種類	過去問	正答
国家一般職	基礎能力試験(pdf)	過去問内
国家専門職（国税専門官）	基礎能力試験(pdf)	過去問内
東京都Ⅰ類B	教養問題(pdf)	正答(pdf)
東京特別区	教養問題(pdf)	–
裁判所事務次官一般職	基礎能力試験(多肢選択式)(pdf)	正答(pdf)

数的推理（数的処理）の勉強は筋トレ？

数的処理の勉強は筋トレに似ています。

少しずつでもいいので、毎日やることが重要です。
ちょっと休むとすぐに筋肉は落ちます。
たまにまとめてやるだけだと、筋肉痛になるだけです。

日々、わずかずつの前進ですが、公務員になったご自分をイメージして継続してください。

最後まで読んでくださって、本当にありがとうございます。
本稿が皆さんのお役に立てば何よりの幸せです。

2024年合格目標｜数的処理対策講座