統計学でよく聞く「分散」と「標準偏差」
本ページにはプロモーションが
含まれていることがあります
代表値とはデータ全体の性質を表した数値のことです。
データの代表値には複数の種類があり、中でも、平均値、中央値、最頻値が主です。それぞれの指標に得意・不得意があり、その使い分けを理解することが重要です。
●平均値（mean, average）：すべての数値を足して、数値の個数で割ったもの。データの中の異常値に影響されやすいことに注意。
●中央値（median）：数値を小さい方から並べたときに、真ん中に来る値。異常値に対して頑丈性を発揮することが利点、データ全体の変動を捉えきれないことが欠点。
●最頻値（mode）：一番頻繁に出現する値。質的データに使える代表値は最頻値のみ。
上記にような代表値だけでは、データ全体の性質をうまく表せないことがあります。平均値と中央値の両方が同じでもデータの分布が異なることもあります。
データのばらつきや広がり具合を示すために、とても重要な指標である「分散」と「標準偏差」をこの記事で解説します。
資料請求でデータサイエンスの基礎が学べる講義を無料プレゼント
・講座（G検定・機械学習・データ分析など） 約3時間分
現役プロ講師によるわかりやすい講義
1分で簡単！今すぐ見れます(会員登録→お申込み→講座視聴)
偏差と分散
改めて、データのばらつきの度合いを定量的に指し示す指標を考慮することが必要です。まず「偏差」と「分散」について紹介します。
「偏差」とは、各データの平均値との違いに着目した値です。ところが、「各データ値と平均の差」を全てのデータについて足し合わせると０になってしまい、使い道がなくなります。そこで代わりに、偏差の２乗を足し合わせて、さらにデータの個数で割った値を使います。この値を「分散」と呼びます。
データの個数で割る理由は… もしそうしない場合、データの個数が増えれば触れるほど参考にする指標が大きくなってしまうからです。
分散（よくσ^2と記載）の値は以下のように計算されます。
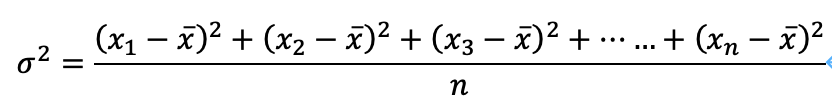
標準偏差
分散をさらに平方根をとったものを「標準偏差」と呼びます。
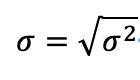
なぜ平方根にするのでしょうか？
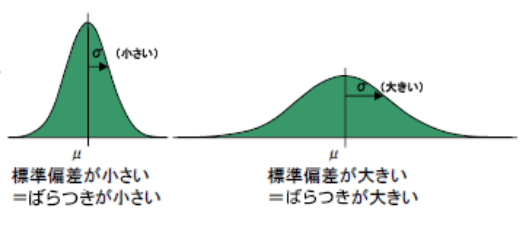
分散は元のデータ（と平均の差）を２乗したものを使っているので、単位が元のデータと異なります。これの平方根をとれば、ばらつきの指標が本来のデータと同じ単位になれるからです。
データのばらつきが大きくなればなるほど分散、標準偏差が大きくなります。
ちなみに、分散が０となるデータは、全てのデータが同じ値であるようなデータです。
資料請求でデータサイエンスの基礎が学べる講義を無料プレゼント
・講座（G検定・機械学習・データ分析など） 約3時間分
現役プロ講師によるわかりやすい講義
1分で簡単！今すぐ見れます(会員登録→お申込み→講座視聴)
実践的な
Python・データ分析スキル
を身に付けたい方へ
何から手をつけたら良いかわからない
独学で挫折したことがある
専門的な内容で身近に相談できる人がいない
このような悩みをお持ちでしたら
AI Academy Bootcampにご相談下さい！
この記事の著者 ヤン ジャクリン
2015年 東京大学大学院 理学系研究科物理学専攻 修了（理学博士）
2015年 高エネルギー加速器研究機構 素粒子原子核研究所（博士研究員）
2017年 株式会社GRI（現職） 講師 兼 分析官
2019年 Tableau Desktop Certified Associate 資格取得
・英検1級
・TOEFL IBT試験満点
北京生まれ、米国東海岸出身（米国籍）、小学高学年より茨城県育ち。
万物の質量の源となるヒッグス粒子の性質を解明し、加速器実験による新粒子発見に関する研究を行い、国際・国内学会発表20件以上、査読論文5件以上。
10年以上に渡り、幅広い年齢層の学習指導を学習塾や大学などで実施（5科目、英会話、受験指導、素粒子物理など）。
現在は、株式会社GRIにて、データ分析官（データ前処理、可視化分析、マーケティング施策の分析 他）
公開講座および法人研修を多数開設。
